|
|
|
 |
| These discussions were abstracted from the book, Bebop to the Boolean Boogie (An Unconventional Guide to Electronics), with the kind permission of LLH Technology Publishing, Eagle Rock, VA, USA. Bebop to the Boolean Boogie provides a superb introduction to a smorgasbord of contempory digital electronics, including atoms, transistors, logic gates, Eskimo counting systems, fuzzbuttons, smoked fish, musical socks, Reed-Müller logic, seafood gumbo, integrated circuits, circuit boards, hybrids, multichip modules, optical interconnects, protein memories & switches, holographic interconnects, superconductors, nanotechnology, and much, much more! |
| Karnaugh Maps Part 2: Minimization Using Karnaugh Maps |
| Karnaugh maps often prove useful in the simplification and minimization of Boolean functions. Consider an example 3-input function represented as a black box with an associated truth table (Figure 3). (Note that the values assigned to the y output in the truth table were selected randomly, and have no significance beyond the purposes of this example.) |
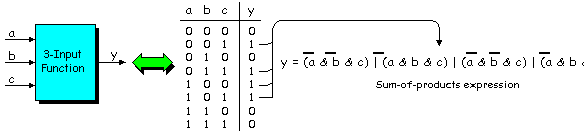
Figure 3: Example 3-input function. |
| The equation extracted from the truth table in sum-of-products form contains four minterms, one for each of the 1s assigned to the output. Algebraic simplification techniques could be employed to minimize this equation, but this would necessitate every minterm being compared to each of the others which can be somewhat time-consuming. (Note that the sum-of-products and product-of-sums canonical forms are introduced in Chapter 9 of Bebop to the Boolean Boogie.) |
| This is where Karnaugh maps enter the game. The 1s assigned to the map's boxes represent the same minterms as the 1s in the truth table's output column; however, as the input values associated with each row and column in the map differ by only one bit, any pair of horizontally or vertically adjacent boxes corresponds to minterms that differ by only a single variable. Such pairs of minterms can be grouped together and the variable that differs can be discarded (Figure 4). |
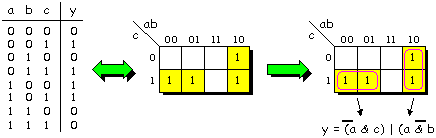
Figure 4: Karnaugh map minimization of example 3-input function. |
|
| In the case of the horizontal group, input a is 0 for both boxes, input c is 1 for both boxes, and input b is 0 for one box and 1 for the other. Thus, for this group, changing the value on b does not affect the value of the output. This means that b is redundant and can be discarded from the equation representing this group. Similarly, in the case of the vertical group, input a is 1 for both boxes, input b is 0 for both boxes, and input c is 0 for one box and 1 for the other. Thus, for this group, input c is redundant and can be discarded. | ||
|
|
 |
|
|
|
|
|
|